Bend or Break: Stiffness, Strength, and Materials for Precision Machine Design
Traditional mechanical engineering is the domain of stress and strength – will a thing break or permanently deform when subject to a given load – static or dynamic, intended or unintended? How can we optimize the design – in terms of cost, weight, or some other performance parameter – and still meet this requirement with an adequate factor of safety?
Precision machine design and optomechanical engineering are the domain of deflection and stiffness – designing a thing so it can hold a position, move to a position, or follow a position with a level of accuracy that is many orders of magnitude smaller than the size of the thing itself.
When Strength Doesn’t Mean Strength
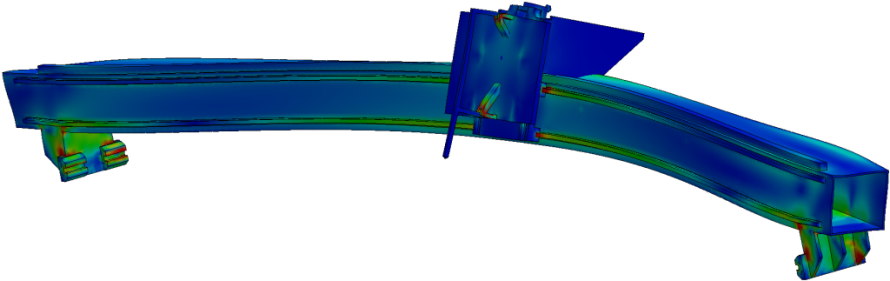
We were helping a client with an example of the latter – a large format cutting system that must follow a complex pattern. The client’s customers value two competing objectives – the accuracy of the finished pattern and the throughput of the system. Higher throughput requires higher velocity and acceleration, but higher accelerations produce higher inertial forces, which increases deflection and reduces accuracy. By solving this conundrum, the client could sell more systems at a higher premium.
The system is a gantry design, with a long beam supporting the cutting head. The client, understanding the price/performance economics better than anyone, asked, what would the deflection be if we made the beam from 7075 aluminum, which has a strength much greater than 6061? And would it be worth the extra cost?
The short version:
- It would make virtually no difference in performance, and
- it would definitely not be worth the cost.
Although 7075 aluminum is stronger than other alloys, it is not stiffer, and stiffness is what determines the deflection of the beam, which is what determines the accuracy of the system.
This confusion is a case of engineers using terminology that is specific to their domain, and clients using the language of everyday life to express the way they experience and understand the world. We say a spring is strong because it takes a high force to compress or that a tree branch is strong enough to stand on because it doesn’t bend under our weight. In a strict engineering sense, that is stiffness, not strength. But the client is not wrong; engineers are the ones who adapt existing words and refine their meaning in a specific context.
As expert consultants, it is our responsibility to listen for and understand what the client truly wants, confirm this understanding with the client, and – in the process – empower the client with greater understanding themselves.
At Practical Precision, our goal isn’t simply to create better designs. It’s to create better, more informed owners of those designs.
The Long Version
Yes, 7075 aluminum is lightweight and strong, making it a great choice for components and structures that are subject to high stresses that might permanently deform or break them. But that is strength in the strict engineering sense of the word. When a number is given for the strength of a metal, it represents the ability of that metal to resist permanent deformation (yield strength, Sy) or breakage (ultimate strength, Su) under a given load and resulting stress state.
In everyday life, we might say a spring is strong because it takes a high force to compress or that a tree branch is strong enough to stand on because it doesn’t bend under our weight. But in a strict engineering sense, that is stiffness, not strength. The material property that relates to stiffness is modulus of elasticity (E), which measures a material’s resistance to deforming under load. In optimizing the beam for accuracy, this is what we care about (stiffness is also highly dependent on form – the way we arrange the material – but more on that later).
7075-T6 aluminum is nearly twice as strong as 6061-T6, but both have virtually the same modulus of elasticity, so there is no significant performance benefit in choosing the more expensive 7075.
The solution is simple then: Instead of selecting a material for strength, select a material with a significantly higher modulus of elasticity, say steel.
That will work, right?
The answer, as you might expect, is that it depends.
Specific Modulus, Stiffness, and Deflection
All other things being equal, simply substituting steel for aluminum will result in a system that is approximately three times stiffer. But it will also be about three times heavier. In many applications, this is not acceptable. The product will become unwieldly and expensive to ship, handle, and install. If it’s a dynamic system, more powerful (and expensive) motors and stronger (and more expensive) drive components may be needed to drive the load.
Even if those trade-offs are acceptable, the increase in stiffness may not translate into the decrease in deflection that is expected.
In applications in which inertial loads are significant, such as self-weight deflection (gravity) or transverse acceleration (as in the case of our gantry beam), the deflection is directly proportional to the mass (and therefore to the density) and inversely proportional to the modulus of elasticity. The ratio of modulus of elasticity (E) to density (ρ), called the specific modulus or specific stiffness, is nearly constant for most metals. So substituting one for another typically won’t change the deflection due to the inertial self-load.
As noted above, steel is about three times stiffer than aluminum, but it is also three times denser. Likewise, 7075 aluminum is slightly stiffer than 6061, but it is also slightly denser. This is generally true: The stiffer a material is, the denser it is. Thus the specific modulus for each is:

Nearly identical.
The maximum deflection of a simply supported beam subject to a uniformly distributed load, such as gravity or another acceleration acting on its own mass, can be calculated as:
 As we see, the only material property that affects deflection is specific modulus, which is the same for most metals. So simply changing material as a brute force method for reducing deflection is usually ineffective.
As we see, the only material property that affects deflection is specific modulus, which is the same for most metals. So simply changing material as a brute force method for reducing deflection is usually ineffective.
Specific Modulus and Natural Frequency
Natural frequency is another critical characteristic of many precision systems. We want to avoid resonances with certain driving frequencies in the system or environment or be above a certain threshold for control systems.
Natural frequency is given by ω.n = √(K/m), where k is the stiffness of the system and m is the mass. The stiffness is proportional to the modulus of elasticity, E, and the mass is proportional to the density, ρ, so again we have a characteristic that is only dependent on the specific modulus of the material, and therefore insensitive to most common material choices.
So How Do We Optimize for Deflection?
Design Form
Like the intuitive example of the spring that we discussed earlier, the more an individual element of metal in the beam is stretched or compressed, the more force it requires. Therefore, we want to arrange the material in a such a way that deflection in the directions we are concerned with requires the maximum change in length of the maximum amount of material. This is why an I-beam is shaped the way it is.
In a static system, where gravity is the principal load and the beam assume a traditional sag in the middle, with the top of the beam in compression, the bottom of the beam in tension, and the middle of the beam (the neutral axis) undeformed, the I-beam would be oriented vertically, so that most of the material (in the horizontal flanges) is being stretched or compressed.
In a dynamic system like the cutting tool, the I-beam would be oriented horizontally to resist the in plane accelerations.
Careful Application of Stiffer (and Denser) Materials
As we’ve shown, simply swapping steel for aluminum often does not have the desired effect. But careful application of stiffer materials can have great benefit, despite having the same specific modulus. This optimization depends on understanding the load path (how a load applied on one part of the structure is transmitted through the mating components and ultimately to “ground”), how that load subjects those intervening components to tension, compression, or bending; and how that translates to deflection at the point of interest.
For example, in the original design of the gantry, the beam was attached to rigid supports, which were attached to thick aluminum plates, which were attached to two linear bearing blocks, which were attached to linear rails on the base frame, which we will consider ground. Bending in large, relatively flat plates far from the point of interest can contribute to unexpectedly large deflections at the point of interest. That was the situation with the gantry.
The quick fix was to change the material of the plate from aluminum to steel. Since the inertia of the plates does not contribute directly to the deflection of the beam the way the inertia of the beam does, this yielded an improvement despite a similar specific modulus.
The longer term, optimized solution was to design a mount that used form to achieve an even greater increase in stiffness for the same weight, and which transferred the inertial loads more directly from the beam to the bearing blocks.
Advanced Materials
As I’ve noted, most metals There are exceptions to this rule of thumb. Beryllium, for example, has a specific modulus nearly 6 times that of aluminum or steel, and AlBeMet 140 (an alloy of aluminum and beryllium) has a specific modules 2.5 times. Beryllium and its alloys, however, are difficult and toxic to machine, with correspondingly high costs. But in demanding applications, such as defense or aerospace applications, that cost is justified.
Carbon fiber composite is another material system with a favorable specific modulus that also has the advantage that the local cross-section and orientation of the plies can be vary according to the local stress state.
Practical Precision has experience designing with both of these material systems.
– Rob Campbell