The advantage of a kinematic mount is that it locates one rigid body relative to another with very high repeatability, without over-constraining the body or introducing instability. It accomplishes this by using the precise number (and arrangement) of contact points needed to allow the desired degrees of freedom – no more and no less. That is the principle of kinematic constraint, which this article will show how to apply in your designs.
A rigid body has six degrees of freedom (DOF). In a Cartesian coordinate system, these include three translations along the orthogonal axes and three rotations about the orthogonal axes. Introducing a point of contact between two rigid bodies eliminates one of the relative degrees of freedom between them. A kinematic mount locates and orients a rigid body using N contact points, to leave the desired number of degrees of freedom:
DOF = 6 – N
More than N points of contact results in uncertainty and instability. We’re all familiar with a table that has an annoying rock. We just want to be able to move the table (translation in x and y) and turn it (rotation about z), which requires N = 6 – DOF = 3 points of contact.
But the table has four legs, the legs are slightly different lengths, and the floor is uneven, so an unknown (indeterminate) and different combination of three legs contact the floor wherever it happens to be.
And the table isn’t designed to be stable on three legs, so when we lean on it, it rocks back and forth. Since the system wasn’t determinate in the first place, as it rocks back and forth – as we put energy into the system – it walks to a new position and orientation.
The Advantage of Kinematic Constraint
This simple analogy illustrates important concepts that apply to precision machine design and optomechanical design. Even an apparently flat surface like a base plate isn’t, at some level, flat. And the four pads on a mating subassembly are not truly coplanar. By bolting them together, we force them to conform, to deform, to strain. This can have a number of ill effects:
- The function of the part may be compromised: Bearing bores that were coaxial in the free form may be misaligned; a mirror on the subassembly may warp.
- Strain energy is built into the system. As it is subjected to operating and environmental loads (shock, vibration, or thermal gradients), this strain energy can be relieved. Bolted connections can loosen. Now performance deteriorates further and faster.
- The initial position is indeterminate. If the system is disturbed, intentionally or unintentionally, it will settle back into a slightly different, indeterminate position.
The advantage of a kinematic mount is that it is not, by definition, over-constrained. We do not build in distortion that can affect performance or strain energy that can cause frustrating change in performance over time.
Position and orientation, as far as the degrees of freedom we choose to control, is also determinate.
And if we carefully select and arrange the our points of kinematic constraint, the mount is also stable and resistant to shock, vibration, thermal effects, and other loads.
The Building Blocks of a Kinematic Mount
There are three fundamental building blocks of kinematic mounting that can be combined in various forms to achieve your design objectives:
- A ball on a surface – 1 point of contact – 5 degrees of freedom (3 rotations, 2 translations)
- A ball in a vee – 2 points of contact – 4 degrees of freedom (2 rotations, 1 translation)
- A ball in a trihedral socket – 3 points of contact – 3 degrees of freedom (3 rotations)
There are variations on these classic forms, as well as truly novel kinematic mounting techniques. But these three are important both for:
- Developing practical applications, and
- Developing your your understanding of kinematic constraint.
The component features do not need to be of perfect size or form[1]: A ball doesn’t need to be a precise diameter; a vee need not be an exact angle; and plane need not be parallel to some reference
But the surfaces should be smooth over the intended range of motion or area of contact.
That said, precision components such as balls and vees are readily available off-the-shelf from vendors like Bal-Tec, if your design can accommodate them (space constraints often require you to roll your own).
[1] This exception applies only to the surface by itself. If it’s combined with other geometry, such as the ball end of an adjustment screw, geometric tolerances such as the concentricity of the ball with the screw axis is important. If it’s off-set, a cyclical variation could be introduced. More on this in a later discussion on adjustments.
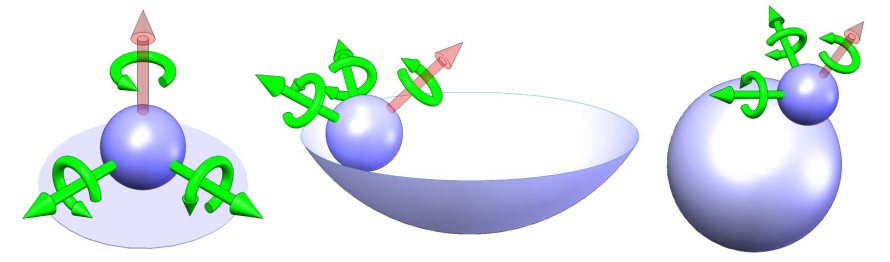
Ball on a Surface – 5 DOF: 3 Rotations, 2 Translations
Figure: A ball on a flat (left), concave (center), or convex (right) surface has 5 degrees of freedom
A ball on a surface has a single point of contact, eliminating the translational degree of freedom normal to the surface.
Typically, we think of a flat surface, but the same applies to most curved surfaces. An exception would be a concave surface with a local radius of curvature smaller than the radius of the ball, which might have multiple points of contact or a circular line of contact.
The ball on a convex surface illustrates the need for some kind of preload to enforce the contact. In many cases, as in the ball on a flat plate, gravity may be sufficient. Preload will be a subject of a later discussion.
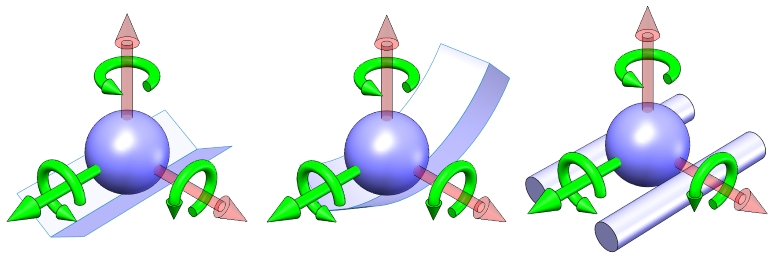
Ball in a Vee – 4 DOF: 3 Rotations, 1 Translation
Figure: A ball in a vee has 4 DOFs: three rotations and translation along the direction of the vee
A ball in a vee has two points of contact, eliminating two translational degrees of freedom. It leaves the translational degree of freedom along the path of the vee and all three rotational degrees of freedom.
As in the case of a ball on a curved surface, the path of a vee need not be a straight line.
And as noted earlier, the precise form of the geometry is not critical. In fact, it need not be a vee at all to achieve the same result. For example, two parallel rods can perform the same function.
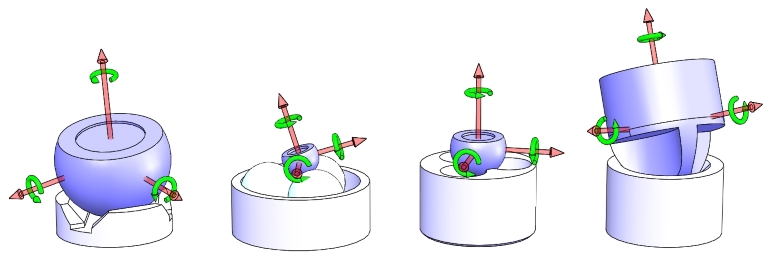
Ball in a Trihedral Socket – 3 DOF: 3 Rotations, 0 Translations
Figure: A ball in a trihedral socket is only free to rotate (3 DOFs)
A ball in a trihedral socket has three points of contact, eliminating all three translational degrees of freedom and leaving only the rotational degrees of freedom. A trihedral socket may not be a familiar component; the article Machining and Modeling Trihedral Sockets for a Kinematic Mount discusses the component as well as alternative constructions for accomplishing the same or approximately the same result.
The ball component in the above examples is no longer a complete sphere:
- In the first three cases, it is ball with a flat
- In the last, it’s a post with a spherical end
This raises an important distinction:
When we refer to the degrees of freedom of a rigid body and eliminating the translational degrees of freedom, as above, that is in reference to being able to define the rigid body’s position and orientation in space.
With the bodies translational DOF fixed, the flat plane can still assume an infinite number of positions in space (but not any position), while the rigid body is rotated about a fixed center.
Putting Them Together
We can combine these building blocks in ways to locate a rigid body with a high degree of repeatability in only the degrees of freedom that we are concerned with, or to allow accurate motion in only the degrees of freedom we choose.
The configurations below demonstrate this concept. We’ll discuss the design and tradeoffs of these and other arrangements – including such considerations as stability, resolution, and interchangeability – in detail in another article.
Figure: A rigid body contacting a surface at 3 points has 3 degrees of freedom, whether that surface is flat or curved
A rigid body with three point contacts on a plane (the left configuration above), is like our stable table, with three degrees of freedom:
- Rotation about the normal to the plane
- Two orthogonal translations on the plane
But we don’t need to confine ourselves to planar geometry. The configuration on the right, a rigid body with three point contacts on a spherical surface, also has three degrees of freedom:
- Again, rotation about the normal to the surface
- Two orthogonal translations tangential to the curved surface
Recognizing and letting go of such self-imposed design constraints can be a challenge, but it can enable novel and elegant solutions. We’ll see more examples of this in other articles.
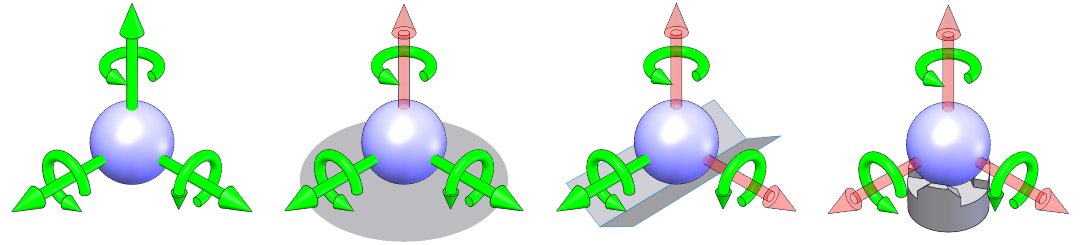
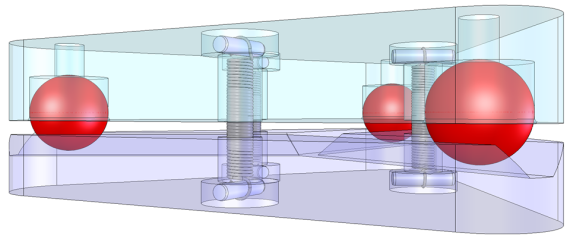
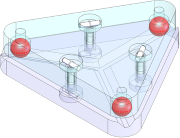
Figure: A Maxwell clamp – three balls in three radiating vees – is fully constrained, but not over-constrained.
The device shown above is commonly referred to as a Maxwell clamp – 3 balls in 3 vees radiating outward. This fixes all six degrees of freedom. When used in such a configuration, it is called a kinematic coupling. Despite not featuring an adjustment, a coupling has a number of practical benefits and uses, including:
- Servicability – It can be disassembled and resassembled, with a very high repeatability. The balls would need to be permanently fixed to the top plate so that they do not get swapped. And since the design is rotationally symmetric, a mark or key is needed to ensure that it is put back the same way.
- Interchangeability – If the top half of the clamp carried a device that required alignment and it was aligned using an external fixture that replicated the bottom half, then different mass-produced devices could be exchanged for one another while maintaining a high level of accuracy in the alignment.
If one or more of the balls were replaced with a ball-end adjustment screw, we could precisely orient the platform. If all three balls were ball-end adjustment screws, we could even precisely translate the platform while maintaining orientation.
We’ll look at the design and tradeoffs of these and other arrangements – including such considerations as stability, resolution, and interchangeability – in detail in another article.




nice description
Thank you for this! I’m learning about exact kinematic constraint in school and these illustrations were really helpful to understand the theory better.